Related Categories
Related Articles
Articles
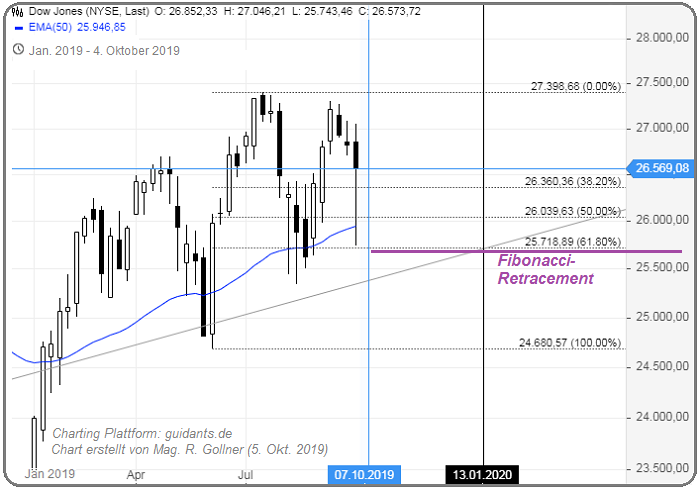
Dow Jones Ind. Average (4. Okt. 2019) &
Fibonacci
Was versteht man unter Fibonacci-Analyse?
Leonardo von Pisa, genannt "Fibonacci", einem italienischen Mathematiker aus dem 13. Jahrhundert, verdanken wir nicht nur die Einführung der indisch-arabischen Zahlen und...
...die ihr zugrunde liegende Mathematik nach Europa. Seine Arbeiten und die nach ihm benannte Fibonacci-Zahlenreihe findet auch in der Charttechnik Verwendung.
Fibonacci entdeckte ein mathematisches Grundprinzip natürlicher Wachstumsprozesse in einem sprichwörtlichen "Feldversuch": Er verwendete dafür das Beispiel der Vermehrung von Kaninchenpaaren innerhalb eines Jahres. Das Ergebnis ist eine unendliche Zahlenreihe, die mit der Zahl 1 beginnt und bei der jeder Term (ausgenommen die ersten beiden) durch Addition von zwei direkt aufeinander folgenden Termen gebildet wird:
1+1= 2; 2+1 = 3, 3+2 = 5; 5+3 = 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987,...
Betrachtet man die Zuwachsrate von einer Fibonacci-Zahl zur nächsthöheren, fällt auf, dass sich diese relativ rasch dem Wert 1,618 annähern (z.b. 89 * 1,618 = 144,002). Dieser Faktor kann nicht nur zur Berechnung einer jeweils folgenden Fibonacci-Zahl verwendet werden. Er beschreibt letztlich die Veränderungsrate aller Fibonacci-Zahlen zur jeweils folgenden und damit das gesamte System. Von Johannes Kepler wurde im 16./17. Jahrhundert dieser Zusammenhang festgestellt; Zuvor hatte er bereits den Zusammenhang zwischen den Fibonacci-Verhältnissen und dem Goldenen Schnitt entdeckt.
Die erste Person, die die Idee hatte, Fibonacci-Zahlen in Finanzwesen anzuwenden, war Charles Dow, der Gründer vom Dow Jones Industrial Average. Er führte aus, dass nachdem der Preis sich mit dem Haupttrend bewegt, kehrt er zur zurückgelegten Entfernung ein Stück zurück, bevor er mit seiner vorherigen Bewegung fortfährt. Er schloss hieraus, dass die Breite des Retracements zwischen 33 % und 66 % war.
Später wurde das Konzept von Ralph Nelson Elliott verfeinert. Er brachte genauere Retracement-Niveaus ins Spiel: 38,2 %, 61,8 % (basiert auf der Fibonacci-Folge) und 50 % (basiert auf den Aktien-Tendenzen).
Was ist der Fibonacci-Retracement-Indikator?
Fibonacci-Retracement ist ein bekanntes Tool der technischen Analyse, das bei Händlern öfters zum Einsatz kommt. Diese Methode wird zur Verfolgung möglicher Unterstützung- und Widerstandsebenen einer Anlage angewendet.
Diese Levels (auch als Fibonacci-Niveaus bezeichnet) sind von den Kennzahlen vorgegeben, die mit der Fibonacci-Folge korrelieren: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,... dies kann ins Unendliche gehen. Jede Zahl ist die Summe der zwei vorhergehenden. Die Folge beinhaltet viele einzigartige mathematische Eigenschaften, die in verschiedenen Bereichen des menschlichen Lebens implementiert werden können.
Die fundamentale Fibonacci-Ratio ist 61,8 %, auch als "der goldene Schnitt" bezeichnet. Sie wird berechnet, indem man eine Zahl durch die nachfolgende teilt (z.B. 34 / 55). Dieses numerische Verhältnis bildet die Grundlage für Retracement-Studien.
Die Fibonacci-Retracement-Niveaus finden sich bei 23,6 % (die Zahl wird durch die andere, drei Stellen höher, geteilt, z.B. 13 / 55), 38,2 % (die Zahl wird durch die andere, zwei Stellen höher, geteilt, z.B. 21 / 55) und 61,8 %. Zwar gehören sie nicht offiziell zur Fibonacci-Ratio, sind 50 %, 78,6 % und 100 % ebenfalls auf der Liste enthalten: aufgrund von unterschiedlichen Tendenzen, die auf diesen besonderen Levels geschehen.
Das Fibonacci-Retracement-Tool wird genutzt, indem man zwei Extrempunkte auf einem Aktienchart nimmt (den tiefsten und den höchsten im Trend) und die Fibonacci-Ratios dafür einsetzt. Diese Vorgehensweise bietet die Möglichkeit, das Ausmaß der Korrektur oder eines Pullbacks "vorherzusagen", bzw. die nächsten Bewegung nach Wahrscheinlichkeit einzuordnen...
Fibonacci in der Chartanalyse, weshalb?, bzw. >>
Wie geht man mit Komplexität (Börse als komplexes System) um?
Wenn die Märkte die Eigenschaften von Dynamik, Aufschaukelung und Komplexität haben, wenn der Beginn und der Ausgang von Entwicklungen nicht planbar und ihre Zukunft mittel- bis langfristig nicht prognostizierbar ist, wie kann man sich dann trotzdem zurechtfinden?
Das Zauberwort heißt Komplexitätsreduktion durch Musterbildung.
Man versucht eine angemessene Vereinfachung des Systems durch Abstraktion zu erreichen. Das ist eigentlich der Kern der Charttechnik. Die klassische Charttechnik greift sich aus dem gesamten Spektrum an Prozessvarianten im Kursverlauf unter anderem diejenigen wiederkehrenden Strukturen heraus, die sie sehr klar erkennen und als Muster beschreiben kann (SKS, Dreiecke, Doppeltop, Trendkanal, Candlestickformationen, etc). Und diese Vereinfachung führt dazu, dass man das Muster wiedererkennen und handeln kann.
Fibonacci-Techniken vollziehen dagegen die Musterbildung auf Basis der Prozesse (Trendverhalten, Bewegung und Korrektur) und auf Basis des relativen, prozentualen Vergleichs der preislichen oder zeitlichen Ausdehnung der Abläufe:
Man arbeitet nicht mit der absoluten Preisveränderung, sondern vermisst die Trends in Form von Relationen. Damit lässt man eine gewisse Unschärfe zu, weil man vereinheitlicht, statt sich mit allen Details der Kursverläufe auseinanderzusetzen. Einfach gesagt: Der Methode reicht es aus, Anfang und Ende einer Bewegung zu kennen, um Aussagen zu treffen. Die Abfolge der Kurse innerhalb dieser beiden Punkte findet nur dann Beachtung, wenn ein zuvor definiertes Fibonacci-Level durchschritten wird oder man die Analyse auf einer niedrigeren Zeitebene durchführt.
"BIG PICTURE sozusagen"
Die Fibonacci-Analyse trennt dabei innerhalb des komplexen Chaos "Börse" methodisch die Prozesse, die Wachstum und zeitlich begrenzte Aufschaukelungstendenzen theoretisch nach sich ziehen können (Trendbewegungen) von denen, die dazu nicht in der Lage sind und denen eine Phase der Stagnation (Korrektur) folgt. Das Unterscheidungskriterium ist das Verhalten der Gegenbewegung, also die Frage, ob und wie weit eine Handelsstrecke korrigiert bzw. retraced wird. Und gerade weil Börse komplex, aber dennoch wachstumsorientiert ist, lassen sich die Definitionen, die Fibonacci als mathematisches Merkmal für Wachstum entdeckte, eins zu eins auf die Börse übertragen. Beispielsweise müssen Kursentwicklungen oder Trendstrecken, die weniger als 61,8 % korrigiert werden, nicht zwangsläufig in eine Trendphase mit exponentiellem oder ungebremsten Kurswachstum münden. Aber sie haben das Potenzial dazu. Während den anderen, mehr als 61,8 % retraceten Spannen dieses Potenzial fehlt.
Und für den Fall, dass sich ein neuer Wachstumsprozeß einstellt, können mittels der Berechnungsmethoden für Wachstum (wie z.B. über Fibonacci-Projektionen) die künftigen Kursniveaus ermittelt werden, an denen dieses Wachstum einen relativen oder absoluten Höhepunkt, also ein temporäres Hoch oder das Ende der Trendbewegung erreicht. Das ist zugleich die Basis und das Erfolgsgeheimnis der Methode.
Sie konzentriert sich damit nicht auf die Details der einzelnen Abläufe, sondern auf deren Rahmenbedingungen. Für trendbestätigende, trendunterbrechende, trendbeendende Entwicklungen werden diese Bedingungen aus der Beobachtung heraus formuliert und in Analyse und Trading umgesetzt. Daher können die Werkzeuge bei kleinen, wenige Euro reichenden Intradaytrends ebenso genutzt werden, wie in jahrelangen Trendphasen, die z.B. zur Vervielfachung einer Aktie führen.
Das bedeutet nicht, dass man ausgehend von einer Trendphase den genauen zukünftigen Verlauf oder den exakten Endpunkt der künftigen Kursentwicklung vorherbestimmen kann. Aber man kann aus dem Verlauf Potenziale ableiten, die unter der Bedingung, dass sich der Trend, also der Wachstumsprozess, fortsetzt, peu á peu abgearbeitet werden. Und nachdem alle Varianten von Bewegung und Korrektur in Aufwärts-, Abwärts- und Seitwärtsmärkten, auf allen Zeitebenen und bei jedem Basiswert auftreten, hat man ein passendes Schema, das universell eingesetzt werden kann, um komplexen Börsen zu Leibe zu rücken.
Dabei ist die Fibonacci-Methode und ihre benachbarten Theoriezweige vielleicht noch nicht der Weisheit letzter Schluss. Vielleicht kommen in Zukunft weitere Erklärungsmodelle und Theorien ins Spiel, die dem Wesen der Märkte noch tiefer auf den Grund gehen. Aber auch dabei wird die Fibonacci-Methode eine der zentralen Säulen in der Theorieentwicklung darstellen. Sie ist eine Vorgehensweise, die die Komplexität, die Wachstumsprozesse und selbstverstärkenden Wechselwirkungen an den Märkten schon sehr genau im Chart erfassen kann: Jede Bewegung der jüngeren Vergangenheit hängt mit den ihr vorangegangen zusammen, unabhängig davon, wer oder was die Bewegung angestoßen hat.
Soweit die Theorie...
Text-Quellen:
https://capital.com/de/fibonacci-retracement
Thomas May
www.thetradingsessions.de/speakers/view/thomas-may



